Quora » 人们弄错的事
BALI @ 2023.01.24 , 01:02 下午Mats Andersson
基准率谬误。
假设我们有一个拥有100万人口的城市，其中有100个恐怖分子，我们有一台恐怖检测机器，可以以99%的准确性确定一个恐怖分子，也就是说它可以在100次中有99次能正确识别出恐怖分子。
这台机器也会出现“误报”。它会以1%的概率将一个“正常”人识别为恐怖分子；也就是说，如果你用它检测100个非恐怖分子，它仍然会标记其中一个。当这个人被机器检测，它会提示“Bing！恐怖分子！”
这个人真正是恐怖分子的可能性是多少呢？正确答案是，大约1%。
可悲的是，同样的数学原理也适用于医学检测，而大多数医生完全不了解这一点。如果有同样100万人口的城市，其中有100个人HIV阳性，而你的检测也能以99%的准确率，但会以1%的概率误认为那些不是HIV阳性的人——那么这意味着如果你拿回测试结果，它是阳性的，它更有可能是你不是艾滋病毒阳性。但大多数医生会说有99%的可能。相当多的人会说它有50%的可能性。有些人甚至会说它是完全确定的。
有人因此自杀。当第二次检测结果证明他们是健康的，为时已晚。
Sarah Alexis
脂肪比碳水化合物更危险，最糟糕的脂肪是饱和脂肪和反式脂肪。
有趣的是许多人混淆了脂肪的类型。
饱和脂肪是链中缺少双键或三键的脂肪酸链，在室温下是固体的。这意味着它们充满了过多的氢，大自然更难分解。还记得听说氢化油对你有害吗？同样适用于此；氢化油具有过多的氢，因此得名，但它们极难分解。
饱和脂肪存在于几种不同的食物来源中(主要是肉类和奶制品)，但它们不是你必须从饮食中完全去除的东西。美国心脏协会建议每天最多摄入13克饱和脂肪。反式脂肪更糟，这些脂肪既可以人工合成，也可以天然存在于食物中。
很多人知道要避免这些，但是为什么呢？
氢化油是一种反式脂肪，强烈建议不要大量食用这种油。这些脂肪会提高你的胆固醇水平，但由于其化学组成，也可能导致动脉阻塞！FDA不建议人们食用反式脂肪，他们鼓励完全限制这些脂肪…它们没有营养价值，只会危害你的健康。
不饱和脂肪食用起来更健康。这些脂肪的碳链中有一个或多个区域含有双键或三键。这在链中产生了弯曲，使体内更容易发生水解。
许多健康专家建议多吃不饱和脂肪，而不是饱和脂肪。
Blaine Jones
很多人不明白地球的倾斜是如何运作的。
地轴的倾斜角度为23.5度，是导致季节的原因。当地球向太阳倾斜时，它会变得更热，反之，当它向太阳倾斜时，它会变得更冷。但大多数人认为地球围绕太阳运行时会主动改变其倾斜度。事实上，地球在一年中不会改变其倾斜度，变化的是地球相对于太阳的位置。
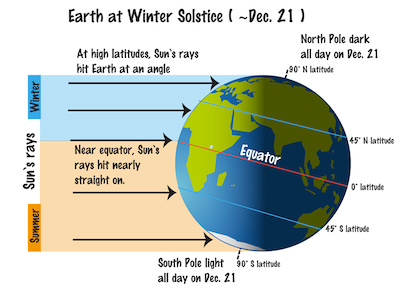
另一个误解是，夏天变热是因为地球更靠近太阳，冬天则相反。事实上，距离的变化几乎不影响温度，真正影响温度的是太阳光线进入大气层的角度。夏季光线更直接，因此更加强烈，而冬季光线则散布在更大的区域，导致热量分布更多，强度更低，使它变得更冷，另外，冬季的阳光必须穿过更多的大气层，这就过滤了更多的热量。
Ajay Patil
人们误解了牛顿第三定律。
"每一个作用力都有一个大小相等方向相反的反作用力。"——这种说法是错误的，如果你不知道后面的部分。
你施加20牛的力在掸子上，它就会移动。但是根据上面的陈述，应该有相等和相反的反作用力。这不会使它的运动完全停止吗？
明白了吗？大小相等方向相反的力会阻止任何运动的发生。
人们不知道的是——"作用力和反作用力总是作用在不同的物体上。"
意思是，如果我推掸子，掸子也会推我。但是由于20N不足以移动我，最终结果是我移动了掸子。
掸子不会对自身施加反作用力。
Babar Khan Javed
“辐射致癌”：从食物到电器都有辐射，我们每天都在接触。
“只有天然的才是好的”：尼古丁是天然的，可卡因在某种程度上也是天然的。
“你能预测地震吗？”：这是每个地震学学生都讨厌的一个问题。
“反社会和反社会性是一回事”：事实上，一个是暴力的精神病患者，另一个是内向的人。
“抗生素能治愈一切”：抗生素有不同的类型，问问微生物学家吧。
“上吐下泻？ 那肯定是流感”：前两者被称为肠胃炎。 流感是一种呼吸系统疾病。
“吃脂肪会让你发胖”：摄入过多的碳水化合物，特别是精制糖，会让你发胖。
“拯救熊猫比拯救蜜蜂更重要”：如果后者灭绝，你会因为食物消失而饿死。