上一期 初中生就能解决的擦桌子问题？

刚上初中的小明用一块边长一分米的正方抹布擦桌子。桌子是边长4分米的正方形。

小明突然想到一个问题。

如果抹布不褶不皱，就是一块正方形不变形。此外，它初始位置是桌子的左上角，且边时刻与对应的桌子边保持平行。现在如果用它抹过桌子的全部点，那抹布的几何中心走过的距离是多少呢？

如果桌子边长是2分米或3分米，我们知道答案分别是3和8分米。

但对4分米的桌子，你能想出移动距离小于15分米的擦法吗？

答案来自 鱼鱼鱼葱卷

这是一个解，移动距离是 10 + 3 * sqrt(2) = 14.2426。

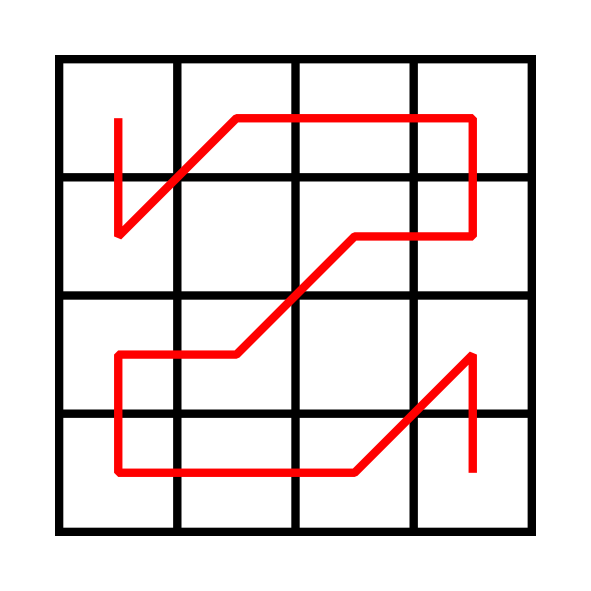
本期问题大有来头。

萨姆·劳埃德是最早的趣题编制大师。18XX年的时候，他就在报纸开设专栏。下面这个问题曾经轰动一时。

当时萨姆为他的趣题悬赏1000美元——考虑时代，那可不是小数目。重赏之下，据说有百万回信，但仅有两人给出了正确答案。当然，这个据说，令人非常生疑——当时全美洲理解无限循环小数的人口有没有百万？(猜测是翻译文献的时候写错了)

好吧，大家试试自己能不能赢下百多年前的1000美元？

题目如下

给你7个数字：0、4、5、6、7、8、9

再给你8个“点”：·、·、·、·、·、·、·、·。

每个数字必须且只能出现一次。点的使用次数，也不能超过8次。

用上面的数字，配合·，组成若干十进制数字。令这些数字相加得到一个最接近82的数(明说了，可以得到82)。

关于“点”，用两种用法。

其一，就是小数点。比如说，1.1。注意，这里允许一种英式数字表示法：0.47可以直接省略0，用“.47”来表示。

其二，“点”在数字的上面，就是所谓的循环小数表示。

PREV : 可编程物质：用光快速变更物体表面的图像
NEXT : 今日好价：微星游戏本