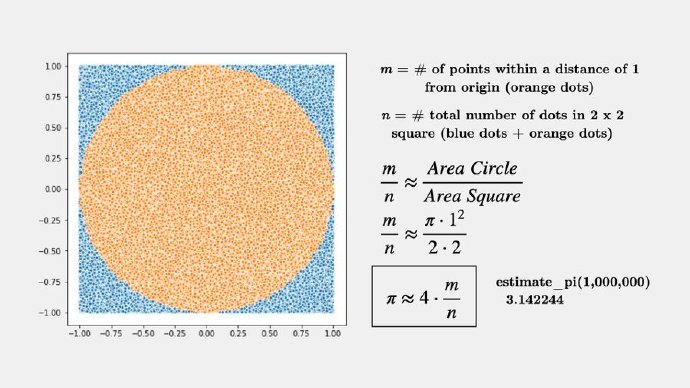
下面是一段简单的python程序。用随机数计算Π。最基础的蒙特卡洛方法应用。

import random

def estimate_pi(n):
m = 0
for i in range(n):
x = random.uniform(0, 1)
y = random.uniform(0, 1)
if x*x + y*y < = 1: m += 1 return 4 * m / n

2014年有两个水论文的物理学家，用步枪在现实场景中完成了上面的算法(就是直接开枪打靶)。

按NewBing提供的信息，论文作者Vincent Dumoulin是蒙特利尔大学计算机科学与运筹学系的博士。他的研究兴趣包括机器学习、深度学习和计算机视觉。他曾在谷歌大脑和Facebook人工智能研究实验室实习，并发表了多篇论文。

另一位，Félix Thouin是蒙特利尔理工学院的博士，他的研究兴趣包括纳米材料、光谱成像和拉曼散射。他曾在加拿大国家科学与工程研究委员会和魁北克省自然科学与工程研究基金会资助下进行研究，并发表了多篇论文。

在我们提及的实验里，他们用莫斯伯格500泵動式散彈槍开了200枪。然后数靶上的着弹点。注意，不是一个靶子，是每枪换一个靶子，然后把所有靶子里的着弹点叠在一个图里。

他们在论文里宣称，他们的工作开拓了借助手边日常工具实施蒙特卡洛方法的可能性。

哦，他们算出来的Π≈3.13。

至于实验目的，他们写道：

“大多数科学家在研究中依赖于预先计算好的π的近似值。

这是有问题的，因为科学进步依赖于一些信息，而这些信息在灾难性事件发生时很可能会遗失，比如在僵尸末日里。

在这种情况下，科学甚至会完全停止。这就激发了我们寻找一种既稳健又易于应用的方法来估计π。 我们首先建立了蒙特卡罗方法的理论框架，包括重要性采样，并提出了一个在这个框架内对π进行概率解释的方法。然后我们介绍了使用基于弹道的建议分布进行重要性采样来计算π的思想，并提出了一种处理未知生成分布的稳健方法。最后，我们将得到的π估计值与真实值进行比较。”

PREV : 血液中的咖啡因水平似乎会影响体脂率和糖尿病风险
NEXT : 今日好价 0321