三位数学家揭示了“上下铺猜想”的错误，挑战数学直觉的局限。

许多数学理论源于直觉，那种“理应如此”的感觉。然而，有时直觉会误导数学家。早期的证据可能无法展现全貌；某个结论看似显而易见，可能却暗藏复杂性。

令人意外的是，三位数学家最近证明了一项在概率论中广为人知的“上下铺猜想”是错误的。这一猜想涉及研究数学图在上下层叠加后如何穿行的方式，看似直观，甚至自然而然。普林斯顿大学的图论学家Maria Chudnovsky表示，“我们的直觉会告诉我们，这个猜想应当成立。”

然而，事实并非如此。上月，这三位数学家宣布找到了一个反例，推翻了这一猜想。这一结果为物理学中一些关于固体材料特性的相关问题提供了新方向，同时也触及了更深层的问题：数学的运作方式。数学家常花费大量精力去证明某些猜想的正确性，而去解构它们的过程往往更加孤独。该团队在找到反例之前失败了多次。这一发现似乎暗示，数学家需要更多地质疑自己的假设。

图上再叠图

20世纪80年代中期，荷兰物理学家Pieter Kasteleyn试图通过数学手段证明一种关于液体在多孔固体中流动的假设。他的研究提出了“上下铺猜想”。

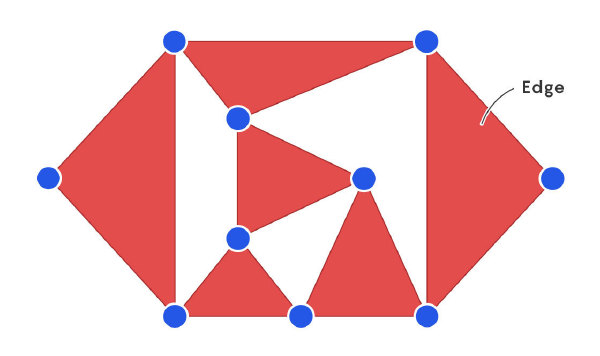
理解这一猜想需从图开始：一组点(称为顶点)，通过线(称为边)连接起来。

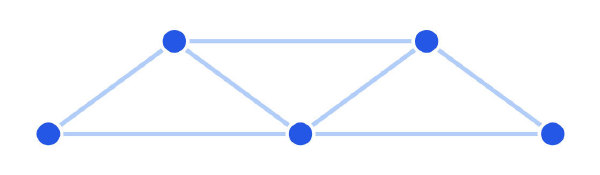
现在，复制该图并将其放置在原图之上。然后，在两图之间添加一些垂直连线(称为额外边)，连接上下图中的对应顶点。这样一来，整体结构便类似于上下铺。

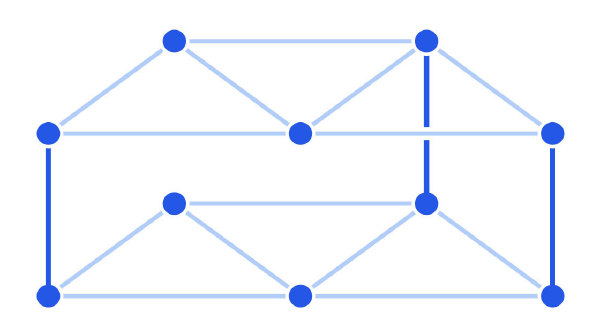
接着，考虑下图中的一条边。抛一枚硬币。如果正面朝上，则删除该边；反面朝上，则保留。对上下两图的每条边重复这个过程。最终，上下铺图会显得不同，但仍然通过垂直边连接。

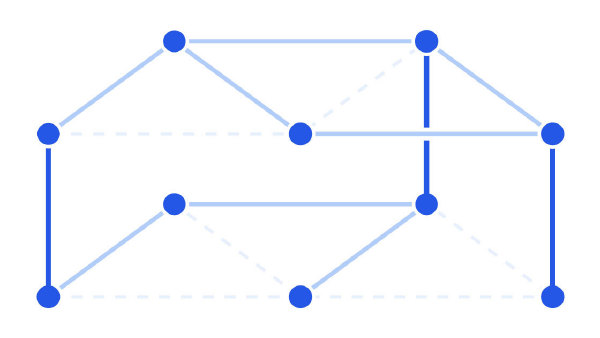
现在，选择下图中的两个顶点。能否通过图中的边从一个顶点移动到另一个，还是说它们已不再连通？对于任意图形，我们都可以计算连通的概率。然后，观察同一对顶点，但其中一个跳到上图的对应顶点。能否找到一条路径从下图的起始顶点到上图的终止顶点？

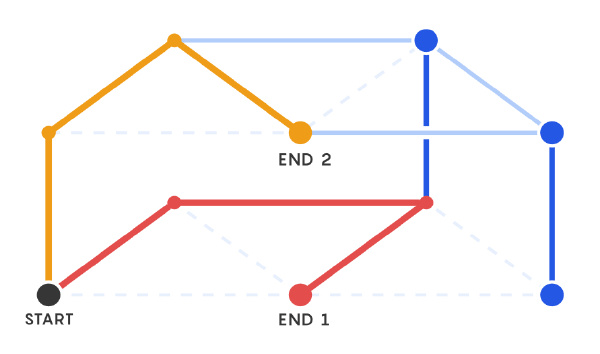
“上下铺猜想”认为，找到仅在下图中连通路径的概率总是大于或等于找到跨层路径的概率。无论起始图是什么，垂直连线多少，或是选择哪对起始和终止顶点，这一结论都适用。

数十年来，数学家一直认为这个猜想是正确的。直觉告诉他们，在一层图中移动要比跨层移动更容易。上到下的额外跳跃应该会显著限制路径的数量。

数学家们也希望“上下铺猜想”成立。该猜想属于渗流理论的一部分。渗流理论研究的是图在随机删除边之后的路径和聚集情况。这类图可以被视为流体在多孔材料中流动的简化模型，就像水在海绵中流动一样。“上下铺猜想”如果成立，将为物理学中的一个假设提供支持，即流体穿过固体的可能性。同时也能为解决渗流物理学中的相关问题提供线索。

然而，要证明“上下铺猜想”成立，远比想象中复杂。

可能的错误

加州大学洛杉矶分校的数学家Igor Pak从一开始就对“上下铺猜想”抱有疑虑。他的学生Nikita Gladkov说：“他一向对陈旧的猜想持怀疑态度。”Pak认为，数学家过于专注于证明某些猜想，而同样重要的进展可以来自“假设这些猜想都是错的。”

Pak对“上下铺猜想”的怀疑还来自其宽泛的表述。Pak质疑它是否真能适用于所有可能的图。“有些猜想有扎实的基础，而有些只是出于愿望。”他认为“上下铺猜想”属于后者。

2022年，Pak开始尝试推翻这一猜想。他花了一年时间多次尝试未果。之后，他指示Gladkov用计算机来进行全方位的搜索，查看所有可能的图。Gladkov意识到这项任务需要复杂的编程，便邀请了从高中起就认识的朋友Aleksandr Zimin来帮助，Zimin目前是麻省理工学院的研究生。“我们在大学时还真有过上下铺的宿舍呢，”Gladkov笑着说。

他们首先手动验证了少于九个顶点的所有图例，发现猜想在这些情况下成立。然而，对于更大的图，情况变得非常复杂，无法穷举所有边被删除或路径形成的可能性。

于是，团队转向了机器学习。他们训练神经网络生成可能偏好上层跳跃的复杂路径。网络生成的许多图例显示，下铺路径只比上铺稍微更可能，但仍未找到相反的例子。

这一方法还有个问题：每一个由神经网络生成的图仍然非常大，数学家无法检查每一个可能的硬币投掷结果。因此，他们只能从这些图的子集里计算上下路径的概率，就像民调通过抽样来预测选举结果。

尽管他们对反例的准确性达到了99.99%的信心，但仍不是100%。团队逐渐怀疑这种方法能否成功，担心它无法说服数学界，也难以被权威期刊认可。“博士生需要的是现实中的工作，不是理论上的争论。”Pak在博客中写道，而Gladkov和Zimin即将找工作。“这也是我们放弃这一方法的原因。为什么要坚持下去，制造争议，不如尝试别的事情？”

于是，他们放弃了计算机方法，但没有完全放下这个问题。在接下来的几个月里，他们转而专注于构建不依赖计算机的理论论证，但始终缺少关键的突破。

突破来自海外

今年6月，剑桥大学的Lawrence Hollom在不同环境下证伪了“上下铺”问题的一个变体。在他的猜想中，研究对象是“超图”。与一般图不同，超图中的一条边可以连接任意数量的顶点。

Hollom找到了一个小型超图反例，每条边连接三个顶点。Gladkov发现了这篇论文，意识到这正是他们所需的关键。“那天我看到论文后读到凌晨三点，简直不可思议。”他回忆道。第二天一早，他和Zimin打电话讨论，考虑是否能将Hollom的超图反例转换为一个普通图，以此推翻“上下铺猜想”。

这并非他们首次讨论将超图转换为图的可能性。去年初，他们在一场演唱会前讨论过这个问题，“当时Red Hot Chili Peppers在演唱，而我脑子里想的却是这个问题，”Gladkov笑着回忆道。后来，他们开发了一套方法，能在特定情况下将超图转换为普通图。

他们意识到，这次可以利用这些方法，改造Hollom的超图。他们将每个三顶点边替换为一个大的点簇和普通边。这构成了一个拥有7,222个顶点和14,422条边的巨大图形。他们运用此前放弃的理论论证证明，在这个图中，上铺路径比下铺路径的可能性高出1/10^6500的微小概率。“上下铺猜想”被证明是错误的。

普林斯顿大学的数学家Noga Alon表示，这一结果显示了不要轻信任何看似显然正确的事物的重要性。“我们必须对那些看似无懈可击的事物保持怀疑。”

尽管Gladkov、Pak和Zimin发现了许多符合猜想的小图例，但这些并不代表复杂图中那些更难预见的情况。

正如Hollom所说：“我们是否真的像我们想的那样理解这一切？”

数学未来的思考

数学家仍然相信流体穿透固体的物理理论，也就是“上下铺猜想”的灵感来源。但他们需要找到其他方法来证明它。

与此同时，Pak认为数学家们需要就数学证明的本质展开更深入的讨论。他们最终在没有依赖计算机的情况下，以理论方式完全证伪了猜想。但随着计算机和AI在数学研究中逐渐普及，数学界在未来或许不得不调整标准。“这是个哲学问题。”Alon表示，“我们如何看待那些高概率成立的证明？”

罗格斯大学的数学家Doron Zeilberger对此持乐观态度。他认为未来数学将接受这类概率证明，“50年内，也许更早，人们将有新的态度。”

然而，另一些人担心这样的未来可能会削弱数学的直觉性和理解力。“也许概率证明会让你失去对真相的真正理解。”Alon指出。

Pak提议，为此类成果设立独立的期刊，以确保这些结果不会在数学界被忽视。但他的主要目标是推动讨论。“没有标准答案，”他说，“我希望学界认真思考，下一次类似的结果是否会被承认。”随着技术继续深入和改变数学领域，这个问题将变得愈加重要。

本文译自 Quanta Magazine，由 BALI 编辑发布。

赞一个 (1)

PREV : 神秘的拉姆齐数：从混沌中发现秩序
NEXT : CAR-T细胞疗法挑战免疫病，“不治之症”有望治愈