无向图是计算机科学中广泛使用的数据结构，由节点(或顶点)和节点之间的边组成，用于捕捉对象及其关系。最小割问题(通常称为“最小割”)是关于图连接性的一个基本结构性问题，询问：断开网络的最廉价方式是什么？更正式地说，给定一个输入图，其中边没有方向(即，图是无向的)，并且与边相关联的是正权重，用于量化边的重要性(例如，道路的容量，关系的强度，端点之间的相似性水平等)，割是节点的两侧的划分。割的大小是连接割两侧节点的边的总权重，最小割问题是找到最小大小的割。

高效解决它一直是算法图论中最基本的问题之一。此外，最小割在实践中具有各种应用，如图像恢复，计算机视觉中的立体和分割，以及网络韧性分析(如道路或电网)。当底层图数据太大并且需要将其划分为更小的组件以便以分而治之的方式处理时，它通常也非常有用。

在算法设计理论中，对于任何需要读取整个输入的问题的渐近复杂度(对于最小割是这种情况)至少是输入大小的线性(因为读取输入所需的时间就是读取输入的时间)。几乎线性时间算法本质上实现了这一下限，因此被普遍认为是可以达到的最佳结果。对于最小割问题，现有的几乎线性时间算法要么是随机的(可能以一定概率输出不正确的答案)，要么只适用于图简单的特殊情况(无法模拟许多实际应用)，因此其最佳复杂性仍然是一个未解决的问题。

在《确定性近线性时间加权图最小割》中，该论文在ACM-SIAM离散算法研讨会(SODA2024)上获得了最佳论文奖，我们设计了第一个几乎线性算法，用于最小割问题，该算法是确定性的(即总是找到正确答案)并且也适用于一般图，从而解决了最小割问题的最佳复杂性。

技术见解

我们的结果是长期研究的结晶，对该问题的算法性进步(包括我们的进步)通常受到图连接性结构发现的启发。特别是，Karger在1996年的一个开创性结果提供了一个几乎线性时间的随机算法，以高概率找到最小割，该工作的关键见解之一是存在一个更小的图，该图在很大程度上保留了所有割的大小。这是有用的，因为可以用更小的图作为输入运行较慢的算法，而慢的运行时间(以较小的图大小为准)仍然可以几乎线性地与原始(较大)图的大小相匹配。事实上，对于最小割问题的许多结构性发现都沿着这个方向，减小问题规模同时保留感兴趣的结构的高层次思想在算法设计中产生了广泛影响。

保留割的图稀疏化

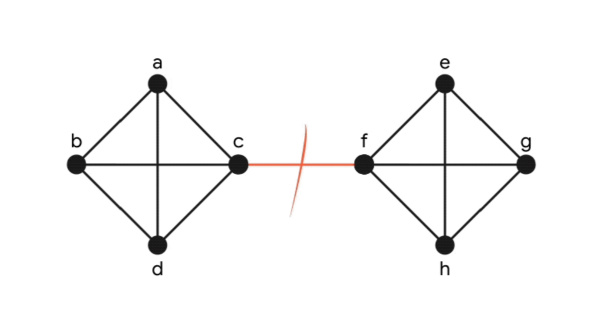
我们首先讨论了Karger更详细使用的结构性见解。从具有n个节点的图G开始，由Benzur和Karger进行的保留割稀疏化证明了存在一个与具有更少边的相同节点集的稀疏加权图G'，使得在G'中，每个割S的大小与G中的大小大致相同，且具有很高的概率。该想法如下图所示，其中原始图由两个完全图组成，通过单个边连接(即哑铃图)，而稀疏化图具有较少但较大权重的边，而所有割大小大约保持不变。

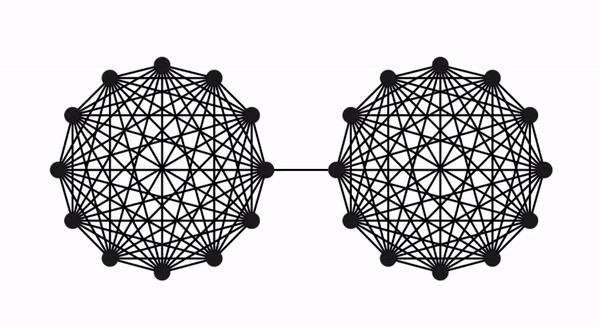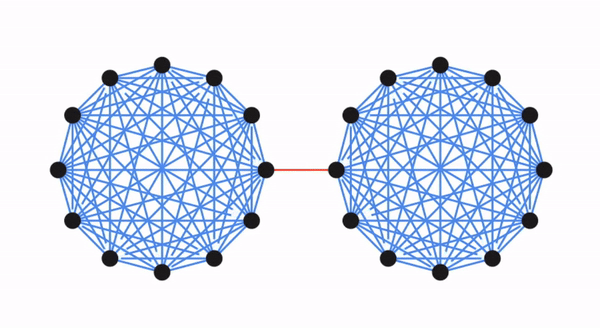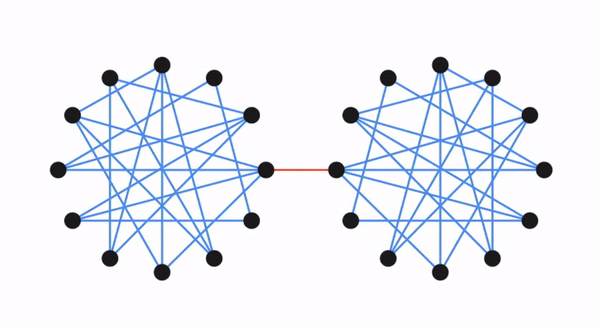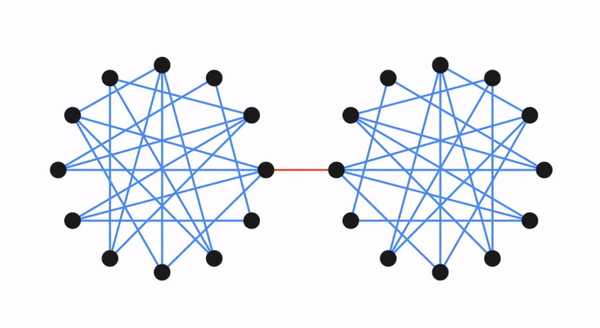
要算法地构建这样一个更稀疏的图，Benzur和Karger使用了独立抽样边的方法，其中每条边在G中以一定概率包含在G'中，并且在G'中的权重按照抽样概率的倒数进行缩放(例如，如果以10%的概率包含，则G中原始权重为1的边在G'中的权重为10)。结果表明，这种非常简单(几乎线性时间)的方法可以成功地构造出保留割的图稀疏化。

保留割的图稀疏化，以及其他几种创造性的算法思想，使得Karger取得了突破性的成果。然而，Karger的算法是一种蒙特卡罗算法，即输出可能具有(小)概率的不正确性，除了将其与实际已知最小割进行比较外，没有其他已知的方法可以确定输出是否正确。自那时以来，研究人员一直在努力解决几乎线性时间确定性算法的问题。特别是，在简单图的情况下，即每对节点之间最多有一条边且所有边权重均为1的图的情况下，Kawarabayashi和Thorup于2015年实现了一个重要的里程碑，即针对简单图的确定性几乎线性时间算法。那项工作的关键观察结果是最小割与另一种重要的图结构，称为低导电割(下文解释)，之间的联系。这种联系在后来的努力中对于在具有一般边权重的图上去随机化Karger算法的构建也是至关重要的，最终导致了我们的结果。

最小割与低导电割的一致性

割S的导电度定义为S的割大小除以S的体积(假设S是划分的较小体积侧且非空)，其中S的体积是S中节点度的总和。低导电割S的概念直观地捕捉了网络中的瓶颈，因为连接S与图其余部分的边数(相对于其体积)很少。图的导电度定义为图中任何割的最小导电度，而具有大导电度的图(也称为展开图)被认为是连接良好的，因为内部没有瓶颈。

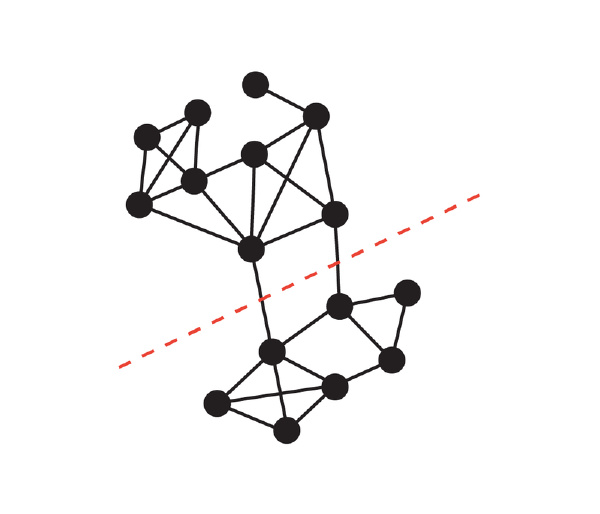
红色虚线代表的切口大小为 2，较小的一边(底部)体积为 24，因此其电导度为 1/12，也就是图形的电导度。

Kawayabarashi和Thorup观察到，在简单图中，任何非平凡割(即两侧至少有两个节点)必须具有低导电度，其中最小节点度较大。在观察到这一点之后，如果能够将图分成连接良好的簇，那么分割必须与每个非平凡最小割一致，这意味着每个簇必须完全位于每个这样的割的一侧。然后可以将每个簇缩减为一个节点，并在所有非平凡最小割都完全保留的较小图上工作。

然而，对于加权图，同样的观察结果不再成立，用于简单图的相同分割在非平凡最小割方面可能不完全一致。尽管如此，Li 2021观察到，这种分割仍然大致与非平凡最小割一致，如下图所示。特别是，对于一个非平凡的割S，存在一个不太不同于S的割S'，使得S'与簇一致。Li进一步观察到，可以利用这种分割的属性来有效地去随机化保留割的图稀疏化的构建。

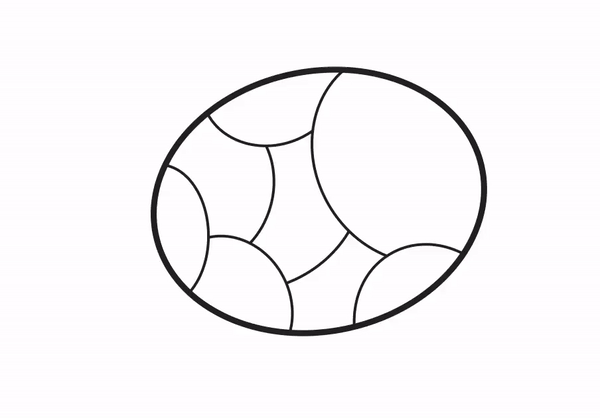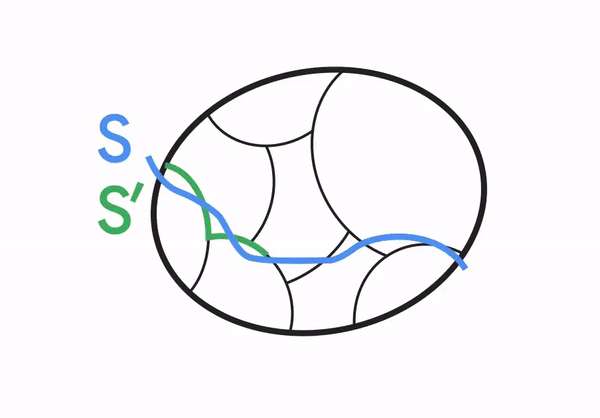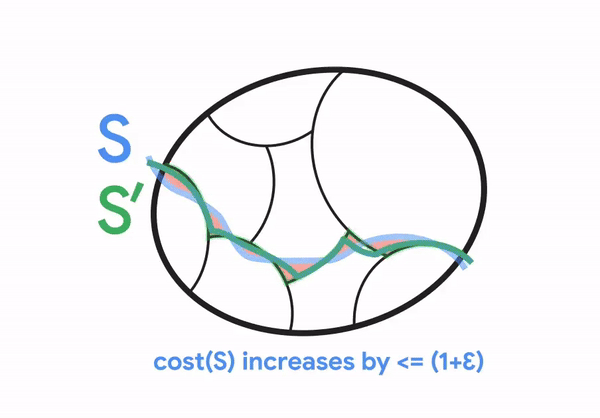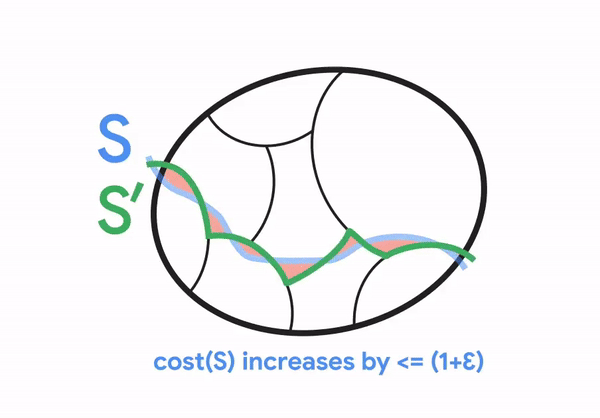
在我们的新结果中，我们设计了一个算法来构建这样一个分割，该分割适用于我们的最小割问题。与Li在先前工作中使用的更通用的现成方法相比，我们量身定制的构造更加精确，因此原始最小割S及其对应的簇一致割S'(如上图所示)的割大小保证更相似。此外，我们的算法比现成方法更快，这是通过改进先前专门用于简单图的聚类技术(由Henzinger、Rao和Wang于2017年开发)以更广泛地适用于加权图而实现的。新构造所实现的更强的精度和运行时间保证最终导致了我们对最小割问题的几乎线性时间确定性算法。

本文译自 google research，由 BALI 编辑发布。

PREV : 现实世界能被模拟到什么程度？
NEXT : 被遗忘的“传呼机战争”