√2作为一个数的定义历程及其在数学发展中的重要意义。

古希腊人曾相信整个宇宙可以用整数及其比例(即我们今天称之为有理数)来描述。然而，当他们研究边长为1的正方形时，发现其对角线的长度无法用分数表示，这打破了他们的信念。

第一个证明这一点的通常归功于公元前6世纪的哲学家Pythagoras，尽管他的著作没有流传下来，对他的了解也很少。尽管如此，加拿大安大略省伦敦市西安大略大学名誉教授John Bell表示，“这是我们所称的数学基础的第一次危机”。

这种危机在很长一段时间内没有得到解决。虽然古希腊人可以证明√2不是有理数，但他们无法解释它是什么。

几个世纪以来，这种模糊性一直存在。文艺复兴时期的数学家在解决代数方程时操作他们所谓的无理数。现代平方根的符号在16和17世纪开始使用。但无理数的存在是否与整数相同，仍然不清楚。

直到19世纪中期，Richard Dedekind等人发现微积分——由Isaac Newton和Gottfried Leibniz在200年前发展起来的——的基础不牢固。Dedekind是一位沉静而有才华的数学家，他准备向学生教授连续函数时，意识到自己无法满意地解释什么是连续函数。

他甚至没有看到函数的正确定义。而这，他认为，需要对数字的工作方式有一个好的理解——这是数学家们似乎理所当然的。他提出了一种使用有理数来定义和构造无理数的方法。

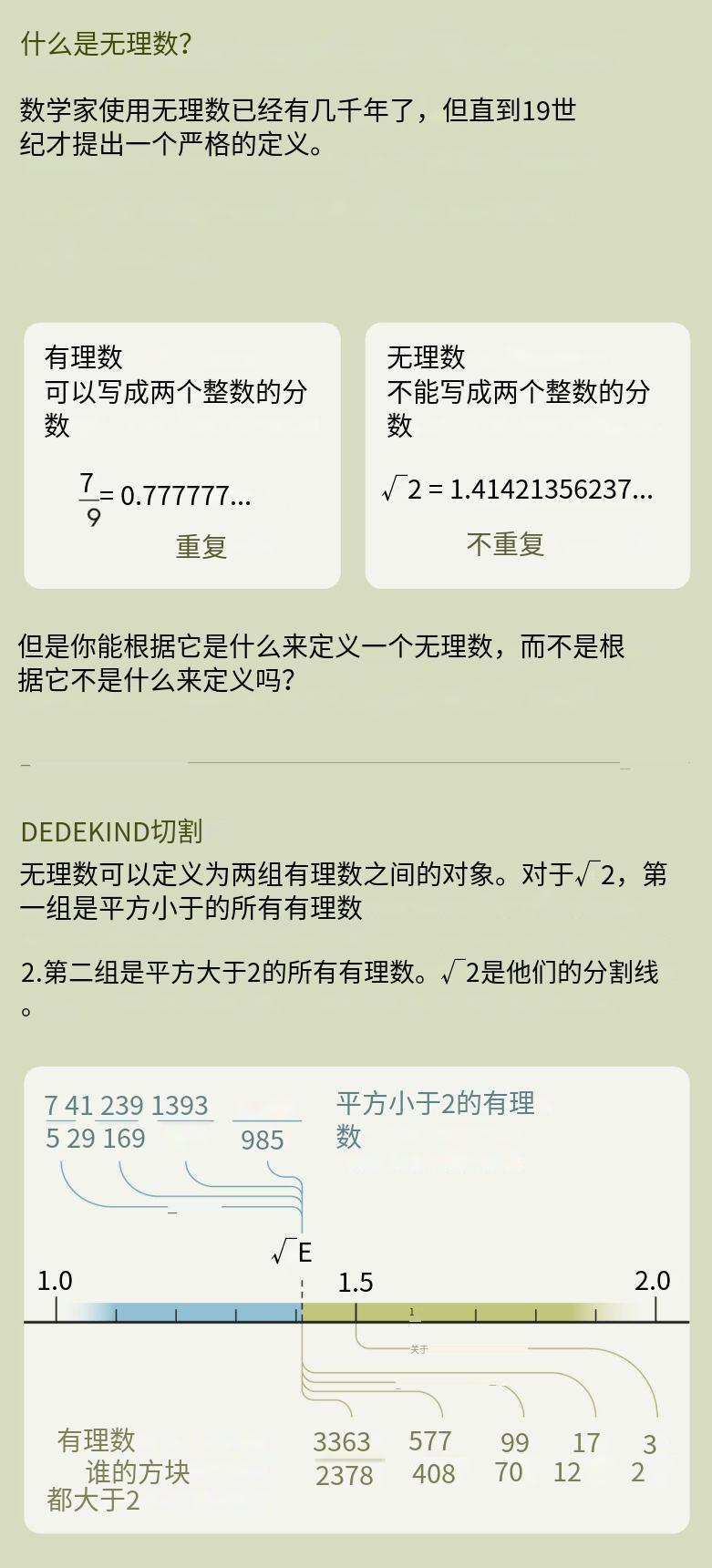
具体来说，将所有有理数分成两组，使得一组中的所有分数都小于另一组。例如，将所有平方小于2的有理数放在一组中，将所有平方大于2的有理数放在另一组中。恰好有一个数填补了这两组之间的空隙。数学家将其标记为√2。对Dedekind来说，无理数是由一对无限的有理数集合定义的，这形成了他所谓的切割。“这是一个非常美妙的想法，”华威大学的Ian Stewart说，“你可以通过描述无理数必须位于的间隙来确定它们。”

Dedekind展示了你可以通过这种方式填充整个数轴，第一次严格定义了现在称为实数的东西(有理数和无理数的结合)。

在Dedekind引入切割的同时，他的朋友和合作者Georg Cantor也开始思考无理数。重叠使他们的关系变得复杂。“他们是好朋友，但也彼此厌恶。他们合作，但也忽略彼此，”以色列开放大学校长、科学史学家Leo Corry说道。

Cantor提出了无理数的另一种定义。他用趋近于某个特定无理值的有理数序列来表示每个无理数。尽管Cantor的无理数最初看起来与Dedekind的不同，但后来的工作证明它们在数学上是等价的。

Cantor的工作引发了他对数的数量的思考。这个问题起初似乎很奇怪。有无数个整数——你总是可以再加一个。推测，这个数集可以是最大的。但Cantor展示了，虽然分数的数量与整数的数量相同，但无理数显然更多。他是第一个意识到无穷大有不同大小的人。

数轴比任何人想象的都要拥挤且奇怪。但数学家只有在改变了视角之后才能看到这一点。

Dedekind的切割可以说是现代数学的起点。“这是数学史上第一个数学家们真正知道他们在谈论什么的节点，”Stewart说。Dedekind和其他人用他的定义第一次证明了微积分中的主要定理——这不仅使他们能够加固Leibniz和Newton建立的基础，还能在其上增添内容。Dedekind的工作使数学家更好地理解序列和函数。据说20世纪初期帮助塑造抽象代数领域的多产数学家Emmy Noether曾告诉她的学生“所有东西都在Dedekind中”。

√2的正式定义为探索新领域开启了新的视野，超越了最初激励Dedekind的微积分话题。正如Stewart所说，“在Dedekind之后，数学家们开始意识到你可以完全发明新的概念。……数学的整体理念变得更加广阔和灵活。”

本文译自 Quanta Magazine，由 BALI 编辑发布。

PREV : 首个不需氧气生存的动物
NEXT : 婴幼儿是如何学会理解语言的