1950芝加哥大学的学生爱德华·纳尔逊Edward Nelson提出了一个看似简单的问题，而数学家用了60年的时间对这个问题软磨硬泡，才一点点撬开真理的外壳。

纳尔逊问道：如果给平面上所有的点都赋予一个颜色，那么至少需要多少种颜色才能保证存在一种着色方法，使得任意两个距离为1的点不同色？

这个问题现在被称为Hadwiger-Nelson问题，或者欧式平面色数问题，它激起了众多数学家的浓厚兴趣，其中包括以论文多产而著称的数学大师PaulErdős。研究人员迅速缩小了答案的可能范围，发现备选答案在4、5、6、7四个数字之中。其他研究人员在随后的几十年中陆陆续续证明了一些部分结果，但没有人能够改进上述范围的上下界。

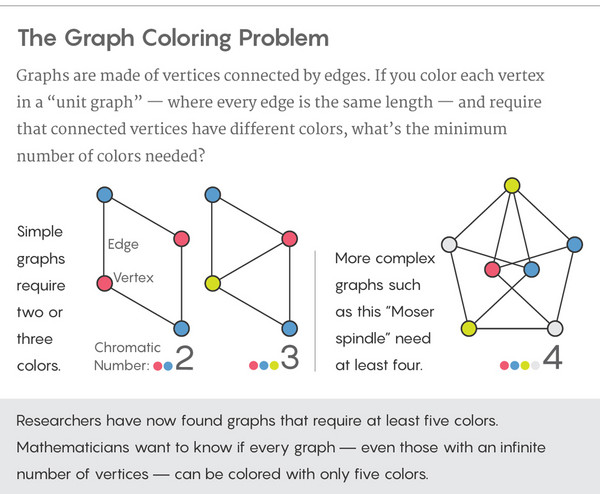
图上是经典的直观证明，为什么2种和3种颜色无法满足条件

上周，生物学家奥布雷德格雷Aubrey de Gray在科学预印本网站arxiv.org上发表了一篇论文，题目是《平面染色数最少是5》(The Chromatic Number of the Plane Is at Least 5)。在这篇文章中，他构造了一种平面结构，该图形不能仅用四种颜色着色。这一发现代表了自引入该问题以来的第一个重大进展。 “我非常幸运，”格雷说。 “并非每天都有人能够发现一个60年都无人解决的问题的答案。”

格雷是一个不太可能的数学开拓者。他是某个科学组织的联合创始人兼首席科学官，该组织旨在开发出长生不老的生物技术。是的，这位生物学家之前给人的印象是语不惊人死不休。实际上，他最为人所知的事迹是，他宣称现在还活着的人将能享受到生物科技的慷慨馈赠，成为历史上第一波活到1000岁的人类。

他在玩棋类游戏的时候，想到了着色数的问题。数十年前，格雷是一名颇具竞争力的黑白棋选手，并且与一些热衷于比赛的数学家同场竞技。他们向他介绍了图论，然后这些东西就在他心里扎下了根，时不时地萦绕在脑海中。

“有时候，我对自己说，如果我能彻底闲下来，我就去研究数学。”去年圣诞节期间，他终于有了充沛的时间。

通过摆弄Hadwiger-Nelson问题，他发现数学家数十年来所做的假设其实是错误的。在他的论文中，格雷向我们表明，一个包含1581个顶点的图至少需要五种不同的颜色来着色。他用到了一种名为Moser纺锤体的数学小工具，以数学家两兄弟Leo和William Moser的名字命名。它是一个有7个点和11条边的配置，其色数为4。通过一个微妙的过程，并借助计算机辅助，格雷将Moser纺锤体和另一些点组合在一起构成基本构件，拼出一个20425个顶点的怪物，这个怪物无法用四种颜色着色。他后来又将构成反例的图的规模缩小到1581个顶点。

许多数学家已经参与到这一挑战之中，目前，最新的记录似乎是826个顶点——现在数学界对Hadwiger-Nelson问题产生了新的兴趣，谁也不晓得最终能将这个著名的问题推进到何种地步。或许，彻底解决？

本文译自 sciencealert，由 majer 编辑发布。
同时参考了quantamagazine上的专栏文章

PREV : 价格感人的折扣化妆品，可能含有大便
NEXT : 新型疫苗可阻断小鼠花生过敏反应