数学家历经65年,证明126维存在奇异扭曲形状,揭示高维空间的独特个性,颠覆直觉,掀开拓扑学新篇章。
在三维世界里,我们对空间的直觉似乎天经地义:无边无际,均匀一致。增加一个维度,不过是多了一个移动方向,空间的本质应该不变。然而,高维空间却像个性格迥异的陌生人,藏着令人费解的秘密。比如,第8维和第24维的球体可以堆叠得异常紧密;某些维度里,球体皱巴巴得像“异类”;而只有第3维能容纳打结的绳子——在更高维度,任何绳结都能在两端固定的情况下被解开。
65年前,数学家们开始追问:哪些维度能孕育出特别扭曲的形状?这些形状怪到无法通过一种叫“手术”的方法变成普通球体。这个问题不仅关乎形状本身,还触及拓扑学核心:不同维度球体之间的关系。多年来,研究者发现,第2、6、14、30和62维存在这种扭曲形状,并且证明其他维度都不可能有此类怪胎——除了一个例外:第126维,始终是个未解之谜。
去年12月,来自上海复旦大学的Weinan Lin和Guozhen Wang,以及加州大学洛杉矶分校的Zhouli Xu,联手破解了这个悬案。他们在网上发布的论文证明,第126维确实能容纳这些奇形怪状。“这是一个漫长的征程,终于画上句号,”牛津大学的Ulrike Tillmann感叹道。哈佛大学的Michael Hopkins则形容这项证明如同“宏大的工程壮举”,让人瞠目结舌。
故事的起点要追溯到1950年代。当时,John Milnor震惊数学界,揭示第7维存在“异类球体”。这些球体在拓扑学看来和普通球体无异——因为拓扑学只关心形状在拉伸或变形后不变的特征。但它们的“光滑”定义却完全不同:一条在普通球体上光滑的曲线,在异类球体上可能显得崎岖不平。Milnor发明了一种叫“手术”的技术,通过切割流形(数学中的一种抽象形状)并缝合新部分,试图将其转化为球体。这项技术后来成为研究流形的基础工具。
想象一个二维的甜甜圈表面(环面),我们可以通过手术把它变成一个二维球面:切掉一块,缝上新部分,确保接缝光滑无棱角。结果是个普通球面——二维不存在异类球体。但在某些维度,手术可能生成普通球体,也可能生成异类球体,甚至还有一种可能:某些流形无论如何都变不成球体。比如,一个被特别“扭”过的环面,就无法通过手术变成球体,它属于完全不同的流形类别。
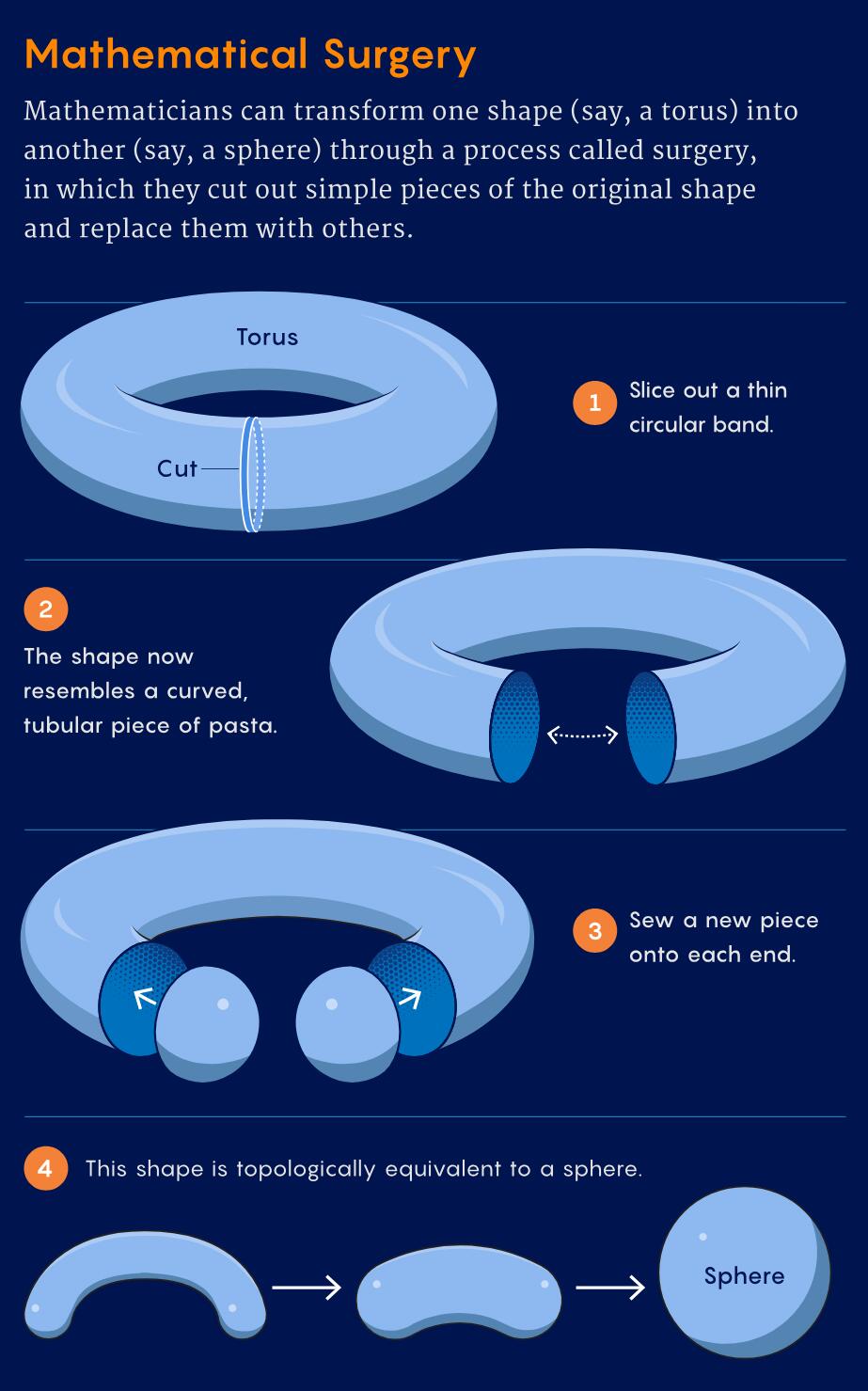
1960年,法国数学家Michel Kervaire提出了一种“不变式”,用一个数字来判断流形能否通过手术变成球体:0表示可以,1表示不行。普通环面的Kervaire不变式是0,而那个扭曲环面是1。Kervaire还发现一个10维流形,奇特到连不变式都没有,意味着它完全无法定义光滑性。这种怪物的存在,让数学家们兴奋不已,纷纷研究不同维度流形的Kervaire不变式。
很快,他们发现第2、6、14和30维存在Kervaire不变式为1的扭曲流形。这些维度有个规律:每个都是2的幂减去2(比如30是2的5次方减2)。1969年,William Browder证明,只有这类维数可能存在此类流形,比如62、126、254维等。数学家们一度以为,所有这类维度都有扭曲流形,甚至有人据此构建了一系列关于异类球体的猜想。但一个“末日假说”始终挥之不去:如果这些维度里没有扭曲流形,那些猜想都会崩塌。
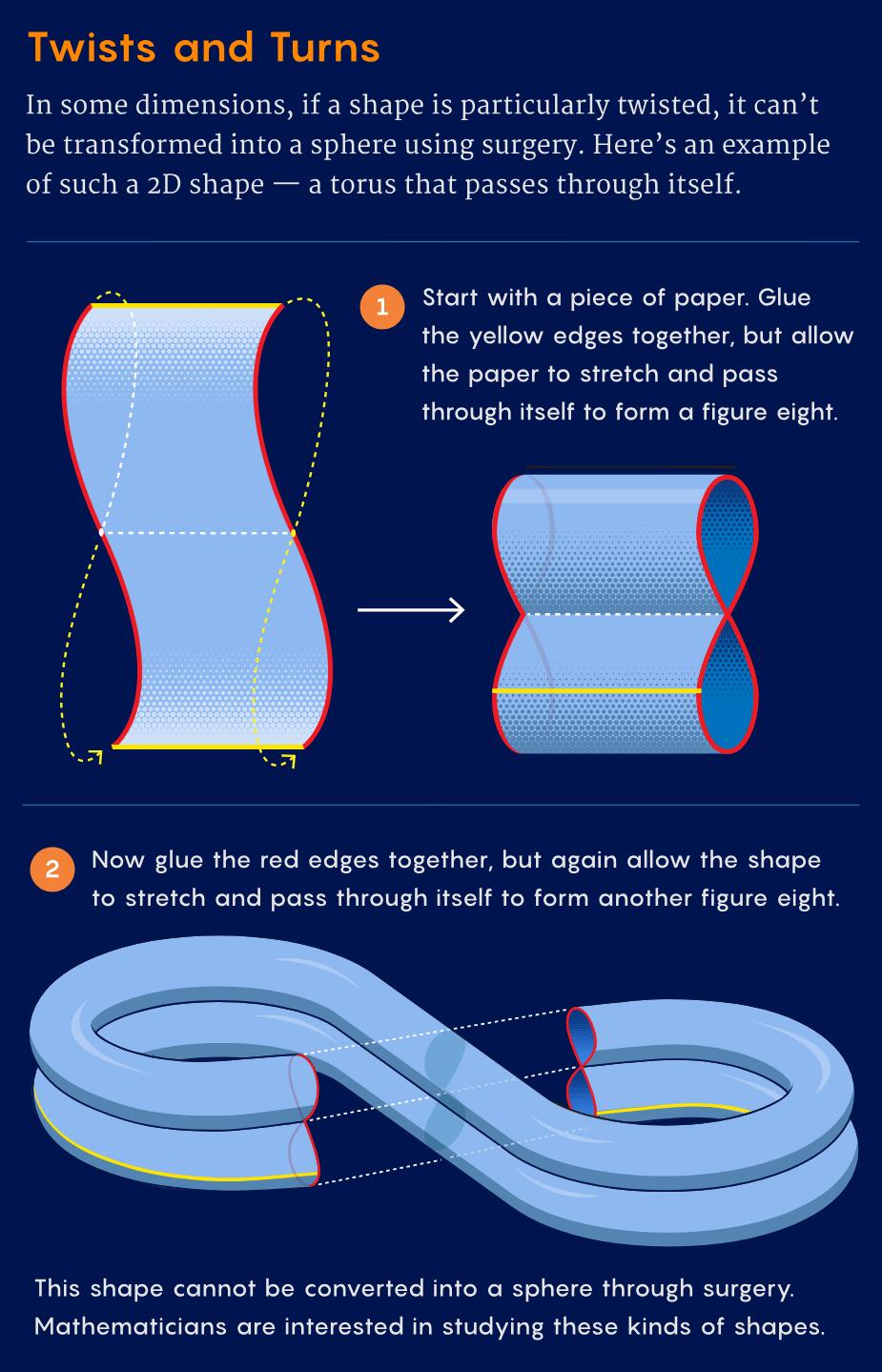
1984年,数学家们确认第62维存在扭曲流形,但更高维度的搜索却屡屡无果。问题渐渐被冷落,直到2009年,Victor Snaith写了一本书,探讨Browder列表中所有维度存在Kervaire不变式为1流形的可能性。他在序言中警告,这可能是一本“关于不存在之物”的书。果不其然,出版后几周,Hopkins等人宣布,末日假说成真:第254维及以上不存在此类流形。唯一悬而未决的,只剩第126维。
2011年,Zhouli Xu作为研究生来到芝加哥大学,计划研究流形的计算问题。他的导师Peter May建议他挑战第126维问题,但西北大学的Mark Mahowald——一位Kervaire不变式专家,甚至将自己的帆船命名为“θj”——认为这太难,劝他先从低维问题入手。尽管如此,第126维始终让Xu魂牵梦绕。
解决这个问题的关键,藏在“稳定同伦群”中。这些群是一组函数集合,描述了高维球面到低维球面的映射。比如,一个44维球面映射到33维球面,会“压扁”11维。每个低维球面上的点,对应高维球面上的一个11维流形。稳定同伦群就像一个装满流形的“桶”,每个桶代表一种映射。
要确定某维度的Kervaire不变式,只需研究该维度的稳定同伦群。但这谈何容易!罗彻斯特大学的Douglas Ravenel直言,这可能是他孙女辈都解不开的难题。于是,数学家们转而借助“亚当斯谱序列”,一个巨大的点阵图谱,记录稳定同伦群的结构。
这个图谱像一本有无限页的书,每页有无限列,每列代表一个维度,每列中的点代表该维度映射的“风味”——比如Kervaire不变式为0或1。翻页就像用更强的望远镜观察流形:早期页面模糊不清,包含许多不应存在的流形;越往后,细节越清晰,直到“无穷页”呈现真相。如果某个点在后续页面消失,说明对应的流形有缺陷,不存在。
Browder曾指出,第126列的一个特定点是关键:如果它存活到无穷页,第126维就有Kervaire不变式为1的流形;否则,只有不变式为0的流形。这个点可能在105种情况下消失。Xu与老友Guozhen Wang合作,开发新的计算方法,又拉上Weinan Lin编写程序,排除了101种可能。接下来一年,他们苦心钻研,逐一否定了最后四种可能。最终,他们确认,这个关键点存活到了无穷页——第126维确实存在扭曲流形。
“这项计算堪称英雄壮举,”Hopkins说。他们的方法或许能帮助数学家进一步绘制这个庞大图谱。然而,证明存在是一回事,构造这些流形又是另一回事。在第2、6、14和30维,数学家已找到具体例子,但在62和126维,这些扭曲流形仍像幽灵,遍布却无迹可寻。“它们占了一半的可能形状,却没人能指认一个,”Tillmann感叹。
如果能构造出62维和126维的扭曲流形,或许能揭示这六个特殊维度(2、6、14、30、62、126)的奥秘。Hopkins期待某种“优美的构造”能解开谜团,“它必须恰到好处,只在这六个数上生效。”最近,Xu和哥本哈根大学的Robert Burklund发现,图谱第三行的一些维度也藏着奇异行为,可能对应新的怪流形。
站在第126维的终点,Xu眺望未来:“还有更多故事,等着我们去探寻。”这些高维怪物的秘密,正慢慢揭开面纱,数学的冒险远未结束。
本文译自 Quanta Magazine,由 BALI 编辑发布。
